Creating Harmony 1: The Basics

Problem:

You don’t know enough about how chords really “work” to understand how to get from one chord to another, and your attempts to create interesting chord progressions never match up to the music that inspires you.

どのようにコードが機能するのか、十分な知識がないので、コードを組み合わせるのが苦手です。好きな曲のコード進行を真似するだけではなくて、自分で新しいコード進行を考えてみたいです。

Harmony is a big topic, and covering the full range of how chords work is beyond the scope of this book. But fortunately, the vast majority of what’s commonly done with harmony in many types of music can be learned with just a bit of background and some basic terms. Here are some of the fundamentals.

ハーモニーは、非常に重要でそれゆえ情報量も莫大なテーマです。本書ではハーモニーの全てを扱うことはできませんが、幸いな事に一般的に行われていることのほとんどは、ちょっとした背景知識を学ぶことで理解することができます。今回は基礎知識を紹介していきます。

Solution:

Most music is considered to be in a particular key. If we say that a song is “in C,” this simply means that the note C sounds to most listeners like the most stable “　 note” for the song. Key can be established in a few ways: either through Repetition and Insistence or, more commonly, through the use of chord combinations that sound, to most listeners, like they want to resolve back to the home note. This sense of tension and resolution is the basis of most successful chord progressions.

基本的に楽曲には「キー」というものがあります。「キー」が「in C」であるといった場合、これは多くのリスナーには「C」の音が一番安定していて、戻るべき場所だと聞こえる、ということを単に示しています。「キー」を確立するためにはいくつか方法があります。例えばCの音を何度も繰り返します。もしくは、もっと一般的な方法として「コード進行」を使って示すこともできます。リスナーがCに戻ろうとしていると感じるようなコード進行を使いましょう。この緊張(Tension)と弛緩(Resolution)のの感覚が効果的なコード進行の基礎となります。

If we continue to assume C is our key note (or tonic), we can then determine the other notes in the scale of the key. The two most common qualities of scales are major and minor. These terms refer to the particular pattern of note distances (or intervals) between the adjacent notes in the scale. The C Major scale contains the following notes (shown in both a MIDI piano roll and conventional notation):

Cをキーノートもしくはトニックと考えた場合、他の音をそのキーのスケールから選んで決定できます。このスケールの中で一番良く出てくる2つの性質は「メジャー」と「マイナー」です。これはスケールの中に含まれる、音と音の距離(音程)を表す用語です。Cメジャースケールは以下の様な音で構成されています。(図参照)

Although the examples in this chapter all use C as the tonic, you can easily transpose the examples in your DAW to try them out in any other key. Every major scale, regardless of starting note, contains seven notes (before repeating the first note again) and the same pattern of intervals between notes. That pattern is a particular combination of half steps (two immediately adjacent notes on the piano keyboard) and whole steps (notes that are two half steps apart):

今回例にあげるのは全てCがトニックの場合ですが、DAWの機能を使って簡単に移調(Transpose)することができます。全てのメジャースケールは、始まる音が違ってはいるものの、どれも7音でできていて、音と音の距離が同じパターンになっています。このパターンは半音と全音組み合わせで出来ています。

Whole - Whole - Half - Whole - Whole - Whole - Half:

全音 - 全音 - 半音 - 全音 - 全音 - 全音 - 半音:

The minor scale contains a slightly different pattern of half and whole steps:

マイナースケールは、すこし異なったパターンを持っています。

Whole - Half - Whole - Whole - Half - Whole - Whole:

全音 - 半音 - 全音 - 全音 - 半音 - 全音 - 全音:

Note:Most DAWs use either only sharps or only flats in the piano roll. For our purposes here, consider D# = Eb, G# = Ab, and A# = Bb.

DAWでは#もしくはbを使って表しますが、D#=EbｍG#=Ab、A#=Bbと同じことを表しています。

Now that we’ve established how major and minor scales are made, we can build chords on each of the notes in the scale. The most common chords are triads, which are built by adding the third and fifth notes above a starting note (or root). For example, in C Major, the triad built on C contains C (the root), E (the third note above C), and G (the fifth note above C). The triad built on A contains A (the root), C (the third note above A) and E (the fifth note above A). Here are the seven triads in C Major:

ここまででメジャースケールとマイナースケールの作り方を理解できたと思うので、次はこのスケールの上にコードを作っていきましょう。まず一般的なコードとしてトライアド(3和音)があります。これは3番目と５番目の音を、最初の音(ルート)に加えたものです。例えばCメジャーキーに含まれる音、Cの音の上にトライアドをつくろうと思うと、C(これがルートです)とE(Cから数えて3番目の音)とG(Cから数えて5番目の音)を使います。他にもAの上にトライアドをつくる場合には、A(これがルートになります)とC(Aから数えて3番目の音)とE(Aから数えて5番目の音)を使います。次の図はCメジャーキーに含まれる7つのトライアドを示しています。

We referred earlier to the terms major and minor as being the quality of the key or scale. The triads in a particular key also have major or minor quality and, as with scales, this is determined by the interval distances between the notes. Major triads have four half steps between the root and the third note, while minor triads have only three. In both major and minor triads, there are seven half steps between the root and the fifth note. With this information, we can analyze and determine the quality of each triad in a particular key, simply by counting semitones.

メジャーとマイナーという用語を先ほどキーやスケール内の音程の性質を表すために使いました。あるキーのなかに含まれるトライアドにもメジャーとマイナーという性質があり、音と音の距離によって決まっています。メジャートライアドは、4つの半音がルートと3番目の音の間にあります。マイナートライアドは、3つの半音がルートと3番目の音の間にあります。メジャーとマイナーどちらのトライアドにも、ルートと５番目の音には7つの半音があります。ですから、この観点からトライアドに含まれる半音の数を数えて、クオリティを知ることができます。

Rather than using specific chord names (such as “C Major”), we can use Roman numerals for this type of chord analysis. This helps to emphasize an important aspect of this theory: Everything discussed here is completely transposable to any key, and all of the harmonic and scale relationships work exactly the same way regardless of which specific note is our tonic. By convention, major triads are labeled with capitalized Roman numerals, while minor triads are written with lower case Roman numerals. Here are the labels for the triads in the C Major scale:

CMajorといった特定のコードネームを使う代わりに、これをローマ数字であわらすことで分析してみましょう。こうすることで音楽理論の重要な側面に気づくことができます。つまり、今まで説明してきたようなことは全て移調できる現象で、あるキーの中のハーモニーとスケールの関係性は、トニックが違うということを除けば、他のどのキーにも当てはまるのです。習慣的にメジャートライアドは大文字で、マイナートライアドは小文字のローマ数字で表します。Cメジャースケール上にできるトライアドの例を見てみましょう

And the triads in the C minor scale:

Cマイナースケール上にできるトライアドは以下のようになります。

If you actually went through and measured the intervals in each of the triads above, you probably noticed that two of these chords don’t fit into either the major or minor pattern. The seven chord in the major scale and the two chord in the minor scale are of a different quality, called diminished. Diminished triads, like minor triads, have three half steps between the root and the third note. But they have only six half steps between the root and the fifth note (as opposed to seven for the minor triad). Diminished triads are labeled with the superscripto after the Roman numeral.

これらのトライアドをよーくみていくと、メジャートライアドでもマイナートライアドでもないコードがあることに気がつくでしょう。メジャースケールの7番目にできるコードと、マイナースケールの2番目にできるコードです。これはdiminishedと呼ばれるクオリティをもつコードです。ディミニッシュド・トライアドはマイナー・トライアドと同じように。3半音をルートと3番目の音の間に持っています。しかし、ルートと5番目の音の間には6半音しかありません。(マイナートライアドは7半音あります。) ディミニッシュ・トライアドは「゜」をローマ数字の後ろにつけて表します。

It may sound surprising, but a huge amount of music, from the Classical period all the way to much contemporary pop and electronic music, uses only the seven chords that exist in a particular key (called the diatonic chords). And many songs use no more than two or three of these chords. But the choice and order of diatonic chords is what determines how the chord progression really sounds. What follows are a few general guidelines that can help you move from one chord to the next (Roman numerals refer to the major scale, but the patterns are similar for minor scales).

驚くかもしれませんが、クラシックミュージックの時代から最近のポップミュージックや電子音楽に至るまで、沢山の音楽がありますが、これなのほとんどにおいて、たった7つのコードが使われているのです。この7つのコードとは今まで説明してきたキーに含まれるコードのことです。(ダイアトニックコードとよばれます。) さらにいえば、かなり多くの音楽では4つ以上のコードは使われていません。しかしどのコードを選ぶか、そしてどんな順番で組合わせるかということが、コード進行のサウンドを決める重要な要素なのです。ではここで、コードからコードへどう進めればいいのか、一般的なガイドラインを示します。(ローマ数字はメジャースケールを想定してつけていますが、マイナースケールにおいても使うことができます。)

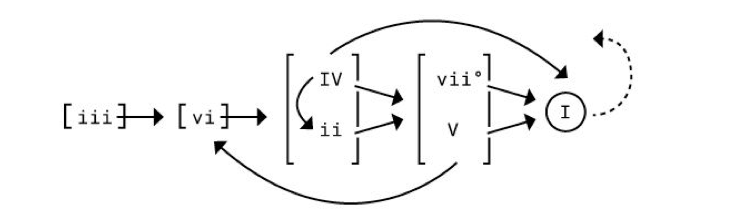
After a I chord, anything is possible; all chords within the key sound equally appropriate after the tonic chord. The V or viio chords sound (to most listeners) like they “want” to resolve back to I (although V can sometimes lead to vi). The ii and IV chords have a tendency to lead towards the V or viio (although IV also commonly leads back to I or to its “partner” ii). The vi chord leads to the ii or IV. And finally, the iii chord has a tendency to be followed by the vi. This series of chord resolutions can be summarized in this figure:

Ⅰコードの後には、どんなコードも続けることができます。トニックコードの後には、キーに含まれるコードであればどんなクオリティのコードでも良いでしょう。ⅤもしくはⅦmb5コードは(多くのリスナーには) Ⅰに帰ろうとしているように聞こえます。(ⅤがⅣに進むこともあります。) ⅡmとⅣはⅤやⅦmb5に進もうとする傾向があります。(ⅣはⅠやⅡmに進むこともあります) ⅥmはⅡmやⅣに進みます。ⅢmはⅥmに進もうとします。これをまとめたのが上の図です。

Using just these guidelines for diatonic triads, you have access to a huge number of usable chord progressions. For example, one of the most common progressions is I - V - vi - IV:

このダイアトニックコードのためのガイドラインを使えば、かなり沢山のコード進行を考えることができます。例えばよく使われるコード進行ですが、Ⅰ Ⅴ Ⅵm Ⅳ などができます。

This is the progression in the verses of Imogen Heap’s “Hide and Seek,” the choruses of Adele’s “Someone Like You,” and many more. In fact, there are countless well-known songs that use this exact progression (“Four Chord Song” by Axis of Awesome is an enlightening mashup of 36 of them).

これはImogen Heap’s “Hide and Seek”のヴァース、Adele’s “Someone Like You”のコーラスで使われているコード進行で、他にも沢山の曲で使われていますね。数えきれないくらい多くの楽曲にこのコード進行が使われています。

Chord progressions that follow these guidelines are said to be functional because each chord functions as a preparation for the next chord in the series. There is, of course, a much wider world of harmonic possibilities available beyond just using diatonic triads. But if you’re interested in creating music that’s within the realm of pop music, you can get quite far using only these seven chords.

このガイドラインにしたがって作られているコード進行は、functional(機能和声)といわれます。なぜなら各コードには、一連のコードの次のコードに進もうとする機能を持っているからです。もちろんダイアトニックコード以外のコードを使って、もっと広いハーモニーの世界に行くこともできます。しかし、ポップミュージックの領域に関心があるのであれば、たった7つのコードを使うだけでも、かなりのことができます。

Side note: A lot of the theory behind the construction of scales and triads may seem like arbitrary, rote memorization. Why did these particular combinations of whole and half steps come to define the scales that are commonly used? Why do certain chords have a feeling of “wanting” to move to other chords? Why do these scales and chords exist at all? Detailed answers are beyond the scope of this book but largely have to do with acoustics: The intervals of the major scale can be derived from fairly simple whole number frequency ratios that correspond to the overtone series. But perhaps even more importantly, much of this theory is descriptive rather than prescriptive: The theory was developed to help explain patterns in music that already existed, rather than to tell composers what they should or should not do in the future.

スケールやトライアドを導き出すためのセオリーは、恣意的で丸暗記するしかないようなものに思えるかもしれません。なぜ全音と半音の特定の組み合わせで、一般的につかわれるスケールを定義できるのでしょうか？なぜコードには他のコードに「進もうとする性質」があるのでしょうか？そもそもなぜスケールとコードというものが存在するんでしょうか？これに関する詳細な回答を本書ではできませんが、しかしこれらの多くは音響現象で説明することができるでしょう。例えばメジャースケールに含まれるインターバルは、周波数的にシンプルな整数比で表すことができ、倍音にも似た性質があります。しかし、もっと重要な事は、セオリーは「説明するために」用意されたもので、守るべき「ルール」のようなものではないということです。セオリーは音楽で実際に起きている現象を説明するために発展し、作曲家がすべきこと、もしくはしてはいけないことを決めているわけではないのです。